Research: Giant lattice softening at a Lifshitz transition in distrontium ruthenate
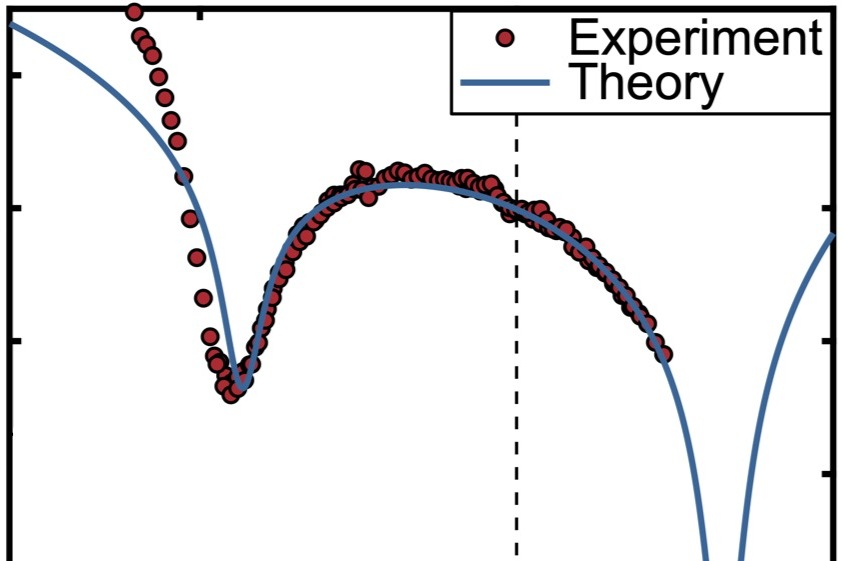
A Fermi surface in a metal separates states of electrons that are occupied at zero temperature from the states that remain unoccupied. This surface is characterised by a specific topology. As a function of the density of electrons or some other parameter this topology can change leading to a quantum phase transition, i.e., a phase transition at zero temperature, which was studied theoretically by Lifshitz already in 1960. Such a Lifshitz transition is accompanied by singularities in thermodynamic quantities that are related to the Van Hove singularities in the electronic density of states. In his original work, Lifshitz already discussed the possibility that such singularities could lead to a softening of the atomic crystal. For a generic metal this softening is however rather weak, but in an effective two-dimensional metal the singularities are expected to be more pronounced.
The material distrontium ruthenate Sr2RuO4 with its layered crystal structure realizes such a two-dimensional metal, and, as shown previously, a Lifshitz transition can be induced by a uniaxial in-plane strain. In a collaboration within the CRC TRR 288 between experimental and theoretical groups, the Young's modulus as a function of applied strain was investigated for this material. Experimentally, it was found that at the critical strain of the Lifshitz transition this modulus indeed exhibits a pronounced softening as envisioned by Lifshitz and changes by more than 10% upon lowering the temperature from 40 K to 4 K. Moreover, it shows a non-linear strain-stress relation violating Hooke's law of elasticity. Members of the Institute of Theoretical Condensed Matter Physics (TKM) and our institute succeeded to explain this anomalous behaviour quantitatively.
Eventually at lowest temperatures, the crystal softening at the Lifshitz transition is expected to result in an elastic instability of the atomic crystal lattice. However, in Sr2RuO4 this instability is preempted by the formation of a superconducting state. It remains an interesting open question whether this crystal instability can be uncovered by suppressing the superconducting phase, for example, by applying a magnetic field.
See also the press release here.
This research was also covered in the research news of Physics 16, 198 (2023).